内挿と外挿

機械学習モデルを構築する上で、 本来データが存在するはずなのにサンプリングできていない（データを取得できていない）空間があると、 その部分の予測精度は落ちてしまう。これについて少し触れてみたい。

データの疎密と誤差の大小

とりあえず実験してみよう。ここでは、\(x\) が \([-5,5]\) の範囲における \(\cos x\) を使ってモデルを構築し、 \(x\) が \([-10,10]\) の範囲の予測を行ってみている。

import numpy as np
import matplotlib.pyplot as plt

# データセット作成
train_X = np.arange(-5, 5, 0.2)[:, np.newaxis]
train_y = np.cos(train_X[:,0])
test_X  = np.arange(-10, 10, 0.2)[:, np.newaxis]
test_y  = np.cos(test_X[:,0])

# 予測モデルの構築
from sklearn.svm import SVR
svr = SVR()
svr.fit(train_X, train_y)

# テストデータに対する予測結果の描画
plt.scatter(train_X, train_y, label="train dataset", color="green")
plt.plot(test_X, test_y, label="true")
plt.plot(test_X, svr.predict(test_X), label="predicted")
plt.legend(loc="lower right")
plt.show()

以下に示したような図が作成されたはずだ。 この図からわかるように、訓練データ（緑点）がある区間は予測誤差は小さい一方、 訓練データが無い区間（両端）は予測誤差が大きくなっている。

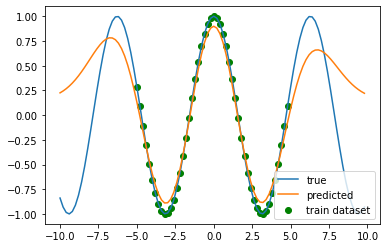
冒頭に述べたように、訓練データに存在していない領域の予測精度は低下してしまうことがわかる。

内挿と外挿

上記で示した例は外挿、すなわち、訓練データの外側（すなわち外挿 extrapolation）の予測を行った。 一方で、学習データの内側に穴があいてしまうこともあるかもしれない。これに対する予測は「内挿 interpolation」と言える。

import numpy as np
import matplotlib.pyplot as plt

# データセット作成
train_X = np.concatenate( 
  [np.arange(-2,-1,0.1), np.arange(1, 2, 0.1)] 
)[:, np.newaxis]
train_y = np.cos(train_X[:,0])
test_X  = np.arange(-3, 3, 0.1)[:, np.newaxis]
test_y  = np.cos(test_X[:,0])

# 予測モデルの構築
from sklearn.svm import SVR
svr = SVR(gamma=.4)
svr.fit(train_X, train_y)

# テストデータに対する予測結果の描画
plt.scatter(train_X, train_y, label="train dataset", color="green")
plt.plot(test_X, test_y, label="true")
plt.plot(test_X, svr.predict(test_X), label="predicted")
plt.legend(loc="upper right")
plt.show()

この結果を見てみると、データが中抜けしている（内挿領域である） \([-1, 1]\) の領域の予測精度はそこまで悪くなく、 一方で外挿領域である \((-\infty, -2]\) や \([2, \infty)\) では予測が大幅に間違っている。

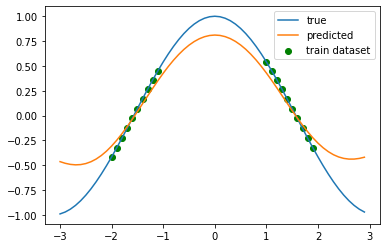
この結果は人間の感覚と合致している。訓練データの並びを見たとき、内挿区間をなめらかにつなごうとすれば自然と山を作る。 一方外挿区間は、この訓練データの並びが \(\cos x\) から来ているのか \(ax^2 + bx + c\) から来ているのかわからないので、 人によって異なる曲線を描くだろう。

なんにせよ、外挿は内挿に比べて、さらに予測精度が悪化する事があるので注意したい。